啪啪啪最优解模型！

万恶之源始于群主。

本文更新于: 2020年4月24日

废话不多说，直接开整。

某天群主突然在群里发了个这个玩意儿。

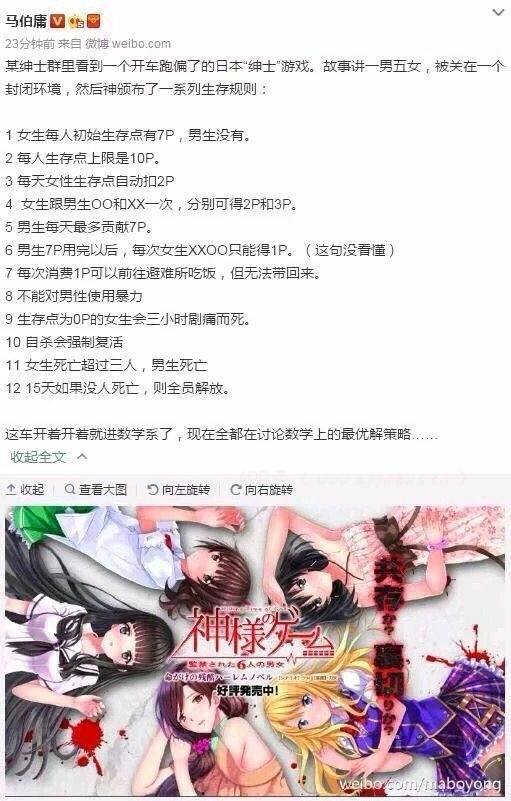
我也是数学专业的，但是学得相对基础，没有深入讨论该问题更加细化的过程，为了节省时间，我省略了数学公式，只编写了代码。该算法在matlab上实现。

因为该情况中的未知量过多，我们可以根据实际情况进行必要的模型假设。

以下是模型假设内容（符号说明包含代码的部分变量）。

模型一：

每顿人人都能吃饭最优模型

假设

1.假设吃饭时间分别为早上7：00-8：00，中午12：00-13：00，晚上20：00-21：00。

2.假设第一天从0点开始。

3.假设男生与女性一次性行为持续时长为30分钟。

4.假设男生与女性两次性行为至少要间隔 30分钟。

5.假设女性与女性发生性行为的持续时长及间隔时长与男性与女性发生性行为的一样。

6.假设睡觉（真正意义上的）时间为21：00 – 6:00，13：00-15：00。

7.假设睡觉时间包含洗漱时间。

8.假设不能同时发生多场性行为，每个小时只能有一对男女或者一对女女。

符号说明

1.向量p分别代表五个女生的p值（即p1，p2，p3，p4，p5）

2.p0代表男生的p值

3.d代表天数。

4. time代表一天的次数。

最优解解释：

即保证性行为最少的情况下，让每个人餐餐都有饭吃。

解法介绍：

即要保证当天所有女生的p>5，男生的p>3即可，男生与女生进行性行为，但由于男生有性爱间隔，所以要保证提前与某女生发生性行为。

根据粗略计算可以得出，一天男女所需要花费的p值为5×5+3=28。一天空闲时间为9小时，因为有时间间隔，所以一个小时可以发生一次性行为。故一天可以产生的p值为7+3×4+5×2=29，其中女生可以用得有p值17，而从上面的结果可以看出，女生每天需要p值为25。故不可以满足需求，所以不能保证每顿都有饭的情况下让所有人存活。

但我们可以退而求其次，假设有一女生死亡，则一天女性需求的p值变为20，但一天女生得到的p值还是17。一天亏3个，就算剩下的女生的初始p值为都10，那么最长11天就会出现第二位死亡者，当然还会接着死亡，但是当死去2名女生后，女生p值的每天需求就变为了3×5=15，而这时女性获得的p值还是17。则对于女生来说，除了生活的必须之外，还能盈余2份p值。

但这都是从p值总数上进行估算的，我们可以用matlab进行编程看一下结果如何。

这个模型非常残酷，因为开始就已经注定了，必定要有两名女生死亡。

由matlab计算结果可以看出，该模型最优解只能让三人存活。（由计算结果可以得到，具体结果可见附件）

代码详情（一共6个文件，五个结果，五个函数内容区别不大，我只给出两个函数的内容。minn函数是为了得到向量中最小元素的索引，p向量元素的个数表示该算法顾及到的女生人数）：

function [y] = GodGame02()
clc;
p = [7,7,7,7,7];
p0 = 0;
mcountsex = 0;
wcountsex = 0;
fid = fopen('GodGame02.txt','wt');
fprintf(fid,'每顿都让5名女生吃，一天九个小时做爱:\n\n');
for d = 1:15
    fprintf(fid,'当前天数为:%d\n啪啪啪情况如下：\n',d);
    mtime = 0;
    wtime = 0;
    time = 0;
    while time < 9
        j = 0;
        n = minn(p);
        for i = 1:length(p)
            if i ~= n
                j = j + 1;
                q(j) = p(i);
            endend
        m = minn(q);
        if m >= n
            m = m + 1;
        endif 1if mtime >= 4
                p(m) = p(m) + 1;
                p(n) = p(n) + 1;
                wtime = wtime + 1;
                fprintf(fid,'女%d号与女%d号进行一次性行为\n',m,n);
            elseif mtime < 3
                p0 = p0 + 3;
                p(n) = p(n) + 2;
                mtime = mtime + 1;
                fprintf(fid,'男生与女%d号进行一次性行为\n',n);
            else
                p(m) = p(m) + 1;
                p(n) = p(n) + 1;
                wtime = wtime + 1;
                fprintf(fid,'女%d号与女%d号进行一次性行为\n',m,n);
            end
            time = time + 1;
            for i = 1:length(p)
                if p(i)>10;
                    p(i) = 10;
                end  
            endif p0 >10
                p0 = 10;
            endendend
    time = mtime+wtime;
    mcountsex = mcountsex + mtime;
    wcountsex = wcountsex + wtime;
    p = p-5;
    p0 = p0-3;
    fprintf(fid,'当天男女啪啪啪次数为:%d\n',mtime);
    fprintf(fid,'当天女女啪啪啪次数为:%d\n',wtime);
    fprintf(fid,'当天啪啪啪总次数为:%d\n',time);
    fprintf(fid,'当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:\n');
    for i = 1:length(p)
        fprintf(fid,'%d ',p(i));
    end
    fprintf(fid,'\n当天男生p值的个数为（已扣除用来吃饭的分数3分）:\n%d\n\n',p0);
    for i = 1:length(p)
        if p(i) <=0breakendendif p(i) <=0breakend
end
countsex = wcountsex + mcountsex;
fprintf(fid,'\n男女啪啪啪总次数为:%d\n',mcountsex);
fprintf(fid,'女女啪啪啪总次数为:%d\n',wcountsex);
fprintf(fid,'所有啪啪啪总次数为:%d\n\n',countsex);
if d ~=15
    fprintf(fid,'未能存活15天，失败');
else
    fprintf(fid,'存活成功');
end
fclose(fid);

——————————————————————————————————————

function [y] = GodGame05()
clc;
p = [7,7,7];
p0 = 0;
mcountsex = 0;
wcountsex = 0;
fid = fopen('GodGame05.txt','wt');
fprintf(fid,'每顿只让3名女生吃，并且做爱次数最少:\n\n');
for d = 1:15
    fprintf(fid,'当前天数为:%d\n啪啪啪情况如下：\n',d);
    mtime = 0;
    wtime = 0;
    time = 0;
    while time < 9
        j = 0;
        n = minn(p);
        for i = 1:length(p)
            if i ~= n
                j = j + 1;
                q(j) = p(i);
            endend
        m = minn(q);
        if m >= n
            m = m + 1;
        endif p(n)<=5||p0<=3if mtime >= 4
                p(m) = p(m) + 1;
                p(n) = p(n) + 1;
                wtime = wtime + 1;
                fprintf(fid,'女%d号与女%d号进行一次性行为\n',m,n);
            elseif mtime < 3
                p0 = p0 + 3;
                p(n) = p(n) + 2;
                mtime = mtime + 1;
                fprintf(fid,'男生与女%d号进行一次性行为\n',n);
            else
                p(m) = p(m) + 1;
                p(n) = p(n) + 1;
                wtime = wtime + 1;
                fprintf(fid,'女%d号与女%d号进行一次性行为\n',m,n);
            end
            time = time + 1;
            for i = 1:length(p)
                if p(i)>10;
                    p(i) = 10;
                end  
            endif p0 >10
                p0 = 10;
            endelsebreakendend
    time = mtime+wtime;
    mcountsex = mcountsex + mtime;
    wcountsex = wcountsex + wtime;
    p = p-5;
    p0 = p0-3;
    fprintf(fid,'当天男女啪啪啪次数为:%d\n',mtime);
    fprintf(fid,'当天女女啪啪啪次数为:%d\n',wtime);
    fprintf(fid,'当天啪啪啪总次数为:%d\n',time);
    fprintf(fid,'当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:\n');
    for i = 1:length(p)
        fprintf(fid,'%d ',p(i));
    end
    fprintf(fid,'\n当天男生p值的个数为（已扣除用来吃饭的分数3分）:\n%d\n\n',p0);
    for i = 1:length(p)
        if p(i) <=0breakendendif p(i) <=0breakend
end
countsex = wcountsex + mcountsex;
fprintf(fid,'\n男女啪啪啪总次数为:%d\n',mcountsex);
fprintf(fid,'女女啪啪啪总次数为:%d\n',wcountsex);
fprintf(fid,'所有啪啪啪总次数为:%d\n\n',countsex);
if d ~=15
    fprintf(fid,'未能存活15天，失败');
else
    fprintf(fid,'存活成功');
end
fclose(fid);

——————————————————————————————————————

function [n] = minn(p) %求向量p最小值的索引
t = p(1);
n = 1;
L = length(p);
for i =2:L
    if p(i) < t
        t = p(i);
        n = i;
    end
end

给其中一个结果：

每顿都让5名女生吃，一天九个小时做爱:

当前天数为:1

啪啪啪情况如下：

男生与女1号进行一次性行为

男生与女2号进行一次性行为

男生与女3号进行一次性行为

女5号与女4号进行一次性行为

女2号与女1号进行一次性行为

女4号与女3号进行一次性行为

女1号与女5号进行一次性行为

女2号与女1号进行一次性行为

当天男女啪啪啪次数为:3

当天女女啪啪啪次数为:6

当天啪啪啪总次数为:9

当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:

5 5 5 5 5

当天男生p值的个数为（已扣除用来吃饭的分数3分）:

当前天数为:2

啪啪啪情况如下：

男生与女1号进行一次性行为

男生与女2号进行一次性行为

男生与女3号进行一次性行为

女5号与女4号进行一次性行为

女2号与女1号进行一次性行为

女4号与女3号进行一次性行为

女1号与女5号进行一次性行为

女3号与女2号进行一次性行为

当天男女啪啪啪次数为:3

当天女女啪啪啪次数为:6

当天啪啪啪总次数为:9

当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:

4 4 4 3 3

当天男生p值的个数为（已扣除用来吃饭的分数3分）:

当前天数为:3

啪啪啪情况如下：

男生与女4号进行一次性行为

男生与女5号进行一次性行为

男生与女1号进行一次性行为

女3号与女2号进行一次性行为

女5号与女4号进行一次性行为

女2号与女1号进行一次性行为

女4号与女3号进行一次性行为

女1号与女5号进行一次性行为

当天男女啪啪啪次数为:3

当天女女啪啪啪次数为:6

当天啪啪啪总次数为:9

当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:

3 2 2 2 2

当天男生p值的个数为（已扣除用来吃饭的分数3分）:

当前天数为:4

啪啪啪情况如下：

男生与女2号进行一次性行为

男生与女3号进行一次性行为

男生与女4号进行一次性行为

女1号与女5号进行一次性行为

女3号与女2号进行一次性行为

女5号与女4号进行一次性行为

女2号与女1号进行一次性行为

女4号与女3号进行一次性行为

当天男女啪啪啪次数为:3

当天女女啪啪啪次数为:6

当天啪啪啪总次数为:9

当天所有女生p值的个数分别为（已扣除吃饭的3分和每天必扣的2分）:

1 1 1 1 0

当天男生p值的个数为（已扣除用来吃饭的分数3分）:

男女啪啪啪总次数为:12

女女啪啪啪总次数为:24

所有啪啪啪总次数为:36

未能存活15天，失败

运行后可得出结果。GodGame05算法可以得出只有3名女生在每顿都能吃饭的情况下可以存活。

最后总结：本模型有缺陷，因为还可以让女生隔几天饿几顿，然后再看看结果如何，但是这样的话，模型需要大幅度更改，因本人能力有限，所以不再做更加详细的结果，而且在此模型也有可能出现诸多错误，请广大读者批评指正。

（ps：男主是真牛皮，饿不死的同时还爽的一批。模型与结果在附件中，有需要自取）

模型1代码以及相应结果

提取码：无

解压码：无复制

下载

本文链接：Click here to view the current URL

声明：本站为个人非盈利博客，资源均网络收集且免费分享无限制，无需登录。资源仅供测试学习，请于24小时内删除，任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集。请支持正版！如若侵犯了您的合法权益，可联系我们处理。

{{userData.name}}已认证

啪啪啪最优解模型！

模型1代码以及相应结果

FolderMove文件、文件夹链接式移动v1.3 / 解决C盘空间不足

TeamViewer客户端被远程控制？深圳网警闹乌龙？

2024年最新iOS 17屏蔽系统更新方法，iPhone、iPad通用！

懒人客服：基于大语言模型（LLM）的智能对话客服工具

skim 小巧轻便的PDF阅读器